本文主要对于 CS231n 课程自带的 Lecture Notes 的一些补充与总结. 建议先看原版的 Lecture Notes，或者可以看知乎专栏中的中文翻译。

另外, 本文主要根据讲课的 Slides 上的顺序来, 与 Lecture Notes 的顺序略有不同.

Lecture 7

Introduction

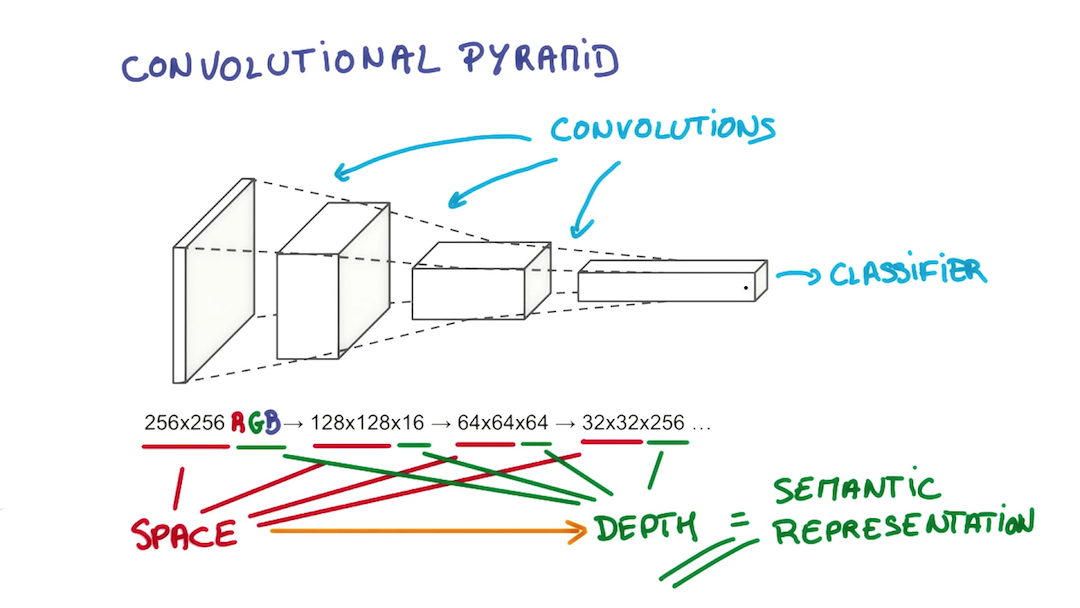
CNN 主要有以下的层(layer):

  • 卷积层 (Conv Layer): 通过不同的 filter 进行卷积操作, 来增加 depth
  • ReLU 层
  • 汇聚层 / 池化层 (Pooling Layer): 进行 down-sampling, 减小空间尺寸
  • 全连接层 (Full-connected Layer): 放在最后进行 classification, 相当于普通的 NN

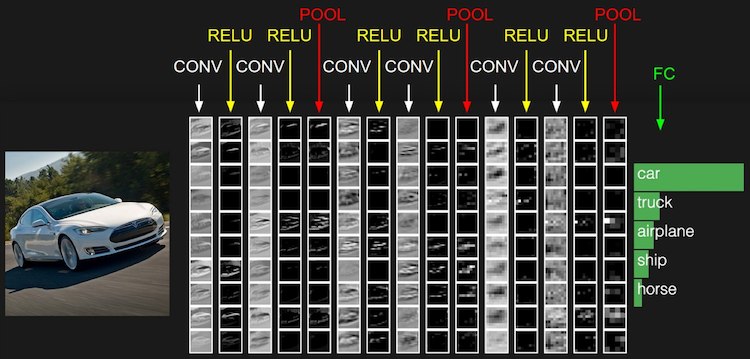
CNN_structure

CNN 相对于 NN 来说, 其结构基于输入数据是图像这么一个假设. 基于该假设, 我们就向结构中添加了一些特有的性质. 这些特有属性使得前向传播函数实现起来更高效, 并且大幅度降低了网络中参数的数量. 这也是 CNN 更适用于图像方面的原因.

Conv layer

主要需要了解以下几个概念:

  • 滤波器(Filter): 又叫卷积核 (Kernel), 尺寸较小 (例如5x5x3). 通过在输入数据上滑动来生成新的 Activation Map / Feature Map.

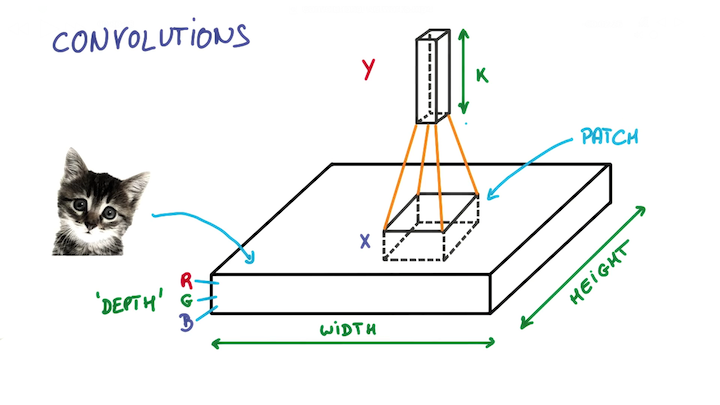
conv_layer_filter

  • 滤波器的深度须与输入数据的深度一致. 也就是说输入 32x32x3 的图像, 其对应的滤波器的尺寸必须是 FxFx3.
  • 下一层的深度取决于这层用了几个滤波器

  • 滤波器的尺寸又称感受野 (Receptive Field)

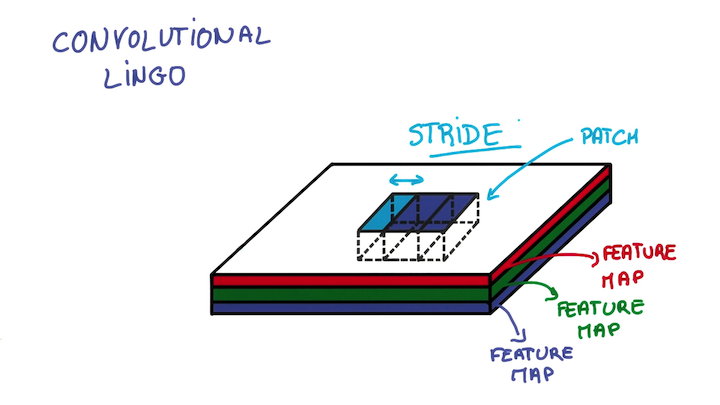
  • 步长 (Stride): 即指滤波器每次移动几个像素. 通常步长为奇数.

CNN_stride

  • 零填充 (Zero-padding): 用来保证滤波器完整平滑地划过输入数据, 不出现非整数的问题. 同时还能够用来保持输入与输出数据具有相同的尺寸, 即令$P=(F-1)/2$.

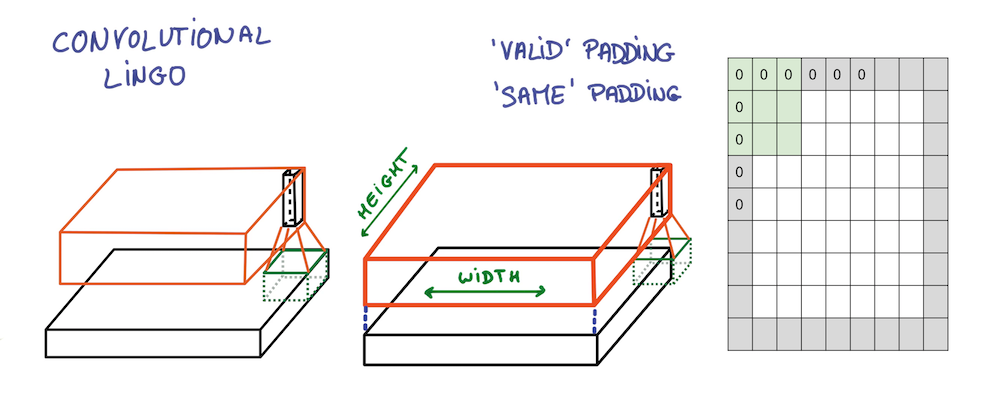
CNN_padding

如是这般, 宽度与高度不断缩小, 深度不断增加, 信息提取得更为抽象.

CNN_layers

总结

  • 输入数据尺寸$W_1 \times H_1 \times D_1$
  • 需要的超参数
    • 滤波器数量$K$, 通常是2的几次幂, 例如32, 64, 128, 512等
    • 滤波器尺寸$F$, 通常为1, 3, 5等
    • 步长$S$, 通常为1或2
    • 零填充数量$P$
  • 输出数据尺寸$W_2 \times H_2 \times D_2$
    • $W_2 = (W_1 - F + 2P) / S + 1$
    • $H_2 = (H_1 - F + 2P) / S + 1$ (通常$W_1=H_1,W_2=H_2$)
    • $D_2 = K$
  • 就参数共享来说, 每个滤波器有$F\cdot F\cdot D_1$个权重参数, 总共有$(F\cdot F\cdot D_1)\cdot K$个权重参数 (weights) 和$K$个偏差参数 (biases).
  • 在输出数据体中, 第$d$层 (尺寸$W_2\times H_2$) 深度切片(depth slice)是由第$d$个滤波器在输入数据体上以$S$为补偿进行有效的卷积, 并且偏移了第$d$个偏差之后得到的.
  • 有时候会有$1\times 1\times D$的滤波器, 其也是有效的. 因为它有深度, 实际上进行的是一个$D$维的点积.

Pooling layer

  • makes the representations smaller and more manageable
  • operates over each activation map independently

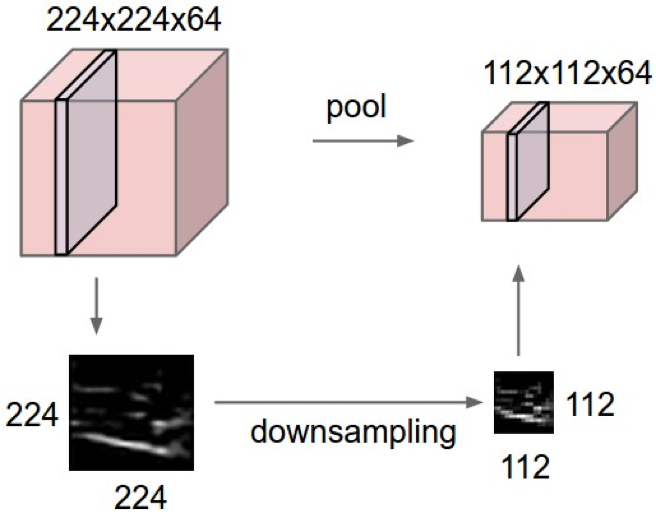
pooling_layer

总结

  • 输入数据尺寸$W_1 \times H_1 \times D_1$
  • 需要的超参数
    • 滤波器尺寸$F$, 通常为2或3
    • 步长$S$, 通常为2
  • 输出数据尺寸$W_2 \times H_2 \times D_2$
    • $W_2 = (W_1 - F) / S + 1$
    • $H_2 = (H_1 - F) / S + 1$ (通常$W_1=H_1,W_2=H_2$)
    • $D_2 = D_1$
  • 由于是固定的计算, 因此没有引入参数.
  • 通常不在汇聚层中使用零填充

Case study

To be continued…

References