An Overview of DCNN Architectures: Efficient Models
Contents
In this post, we discuss the computally efficient DCNN architectures, such as MobileNet, ShuffleNet and their variants.
| Architectures | Resources |
|---|---|
| ResNet | [paper] [code (pytorch)] |
| ResNeXt | [paper] [code (lua, official)] [code (pytorch)] |
| MobileNet | [paper] [code] |
| MobiletNet V2 | [paper] [code] |
| ShuffleNet | [paper] [code] |
| ShuffleNet V2 | [paper] [code] |
| SqueezeNet | [paper] [code] |
| SqueezeNeXt | [paper] [code] |
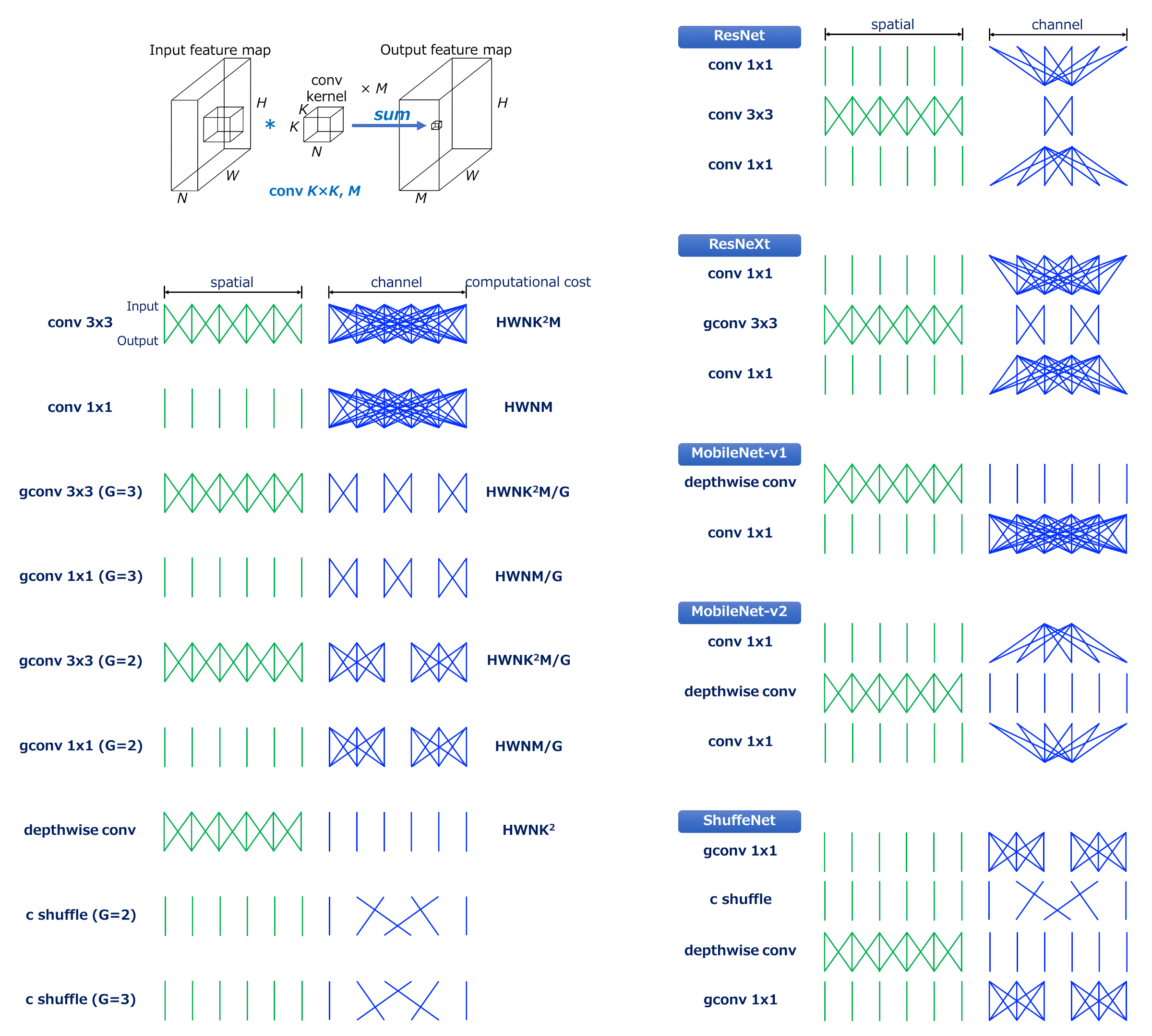
Convolution Operation and Its Variants
卷积操作 (Source: Yusuke Uchida’s blog post)
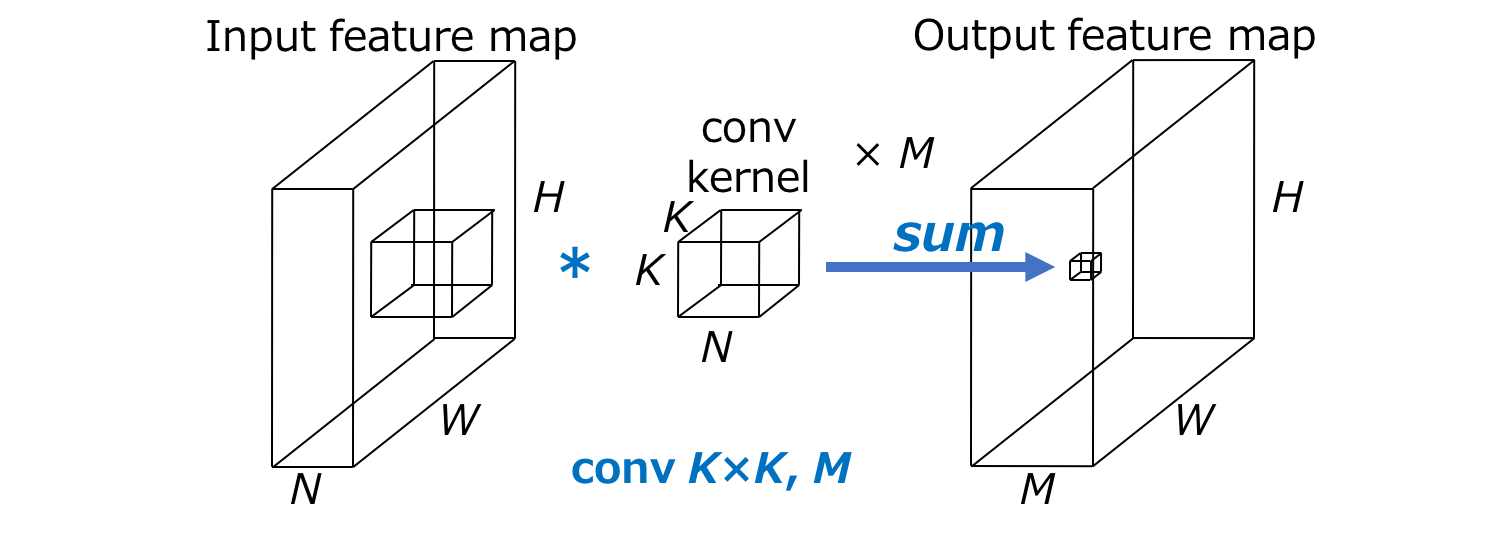
首先来回顾一下卷积操作的计算成本的表示方式。给定以下条件:
- 输入:尺寸为H\times W\times N的feature map
- 卷积:M个K\times K\times N大小的卷积核
- 输出:尺寸为H\times W\times M的feature map
则卷积操作的计算成本为HWNK^2M。可以看出,该计算成本主要受限于:
- 输出feature map的空间尺寸H\times W
- 卷积核尺寸K\times K
- 输入与输出的channel数量N与M
一般来说,输出feature map的尺寸是无法改变的,所以efficient models主要是在第2、3点上做文章。
Standard Convolution
基本的卷积指的是同时在空间(H与W方向)与通道(C方向)上进行卷积操作,其操作成本即为上述的HWNK^2M。
Conv 3x3

3\times 3卷积操作 (Source: Yusuke Uchida’s blog post)
3\times 3的卷积操作如上图所示,可以看出,在空间与通道上都是稠密的连接,其计算成本为9\times HWNM。
- 空间上,output map上的每一点都与input map上的9个点(图中只表现了3个)相关联
- 通道上,output map的每个通道都与input map上的所有通道相关联
Conv 1x1

1\times 1卷积操作 (Source: Yusuke Uchida’s blog post)
1\times 1的卷积又称为pointwise卷积,主要作用是改变input map的通道数量,“融合”各通道的信息。其计算成本为HWKM,是3\times 3卷积的$1⁄9$。
- 空间上,output map上的每一点都只与input map上的一个点相关联
- 通道上,与3\times 3卷积类似,output map的每个通道都与input map上的所有通道相关联
Grouped Convolution

G=2时的3\times 3分组卷积操作 (Source: Yusuke Uchida’s blog post)

G=3时的3\times 3分组卷积操作 (Source: Yusuke Uchida’s blog post)

G=2时的1\times 1分组卷积操作 (Source: Yusuke Uchida’s blog post)

G=3时的1\times 1分组卷积操作 (Source: Yusuke Uchida’s blog post)
分组卷积是基本卷积的变种,主要是将input feature map的通道分组进行卷积,各个组之间卷积操作相互独立,最后再将各个组的结果连接起来。
- 令G代表分组数量,则其计算成本为HWNK^2M/G,是基本卷积的1/G
- G越大,则在通道上的卷积操作越稀疏
Depthwise Convolution

Depthwise卷积操作 (Source: Yusuke Uchida’s blog post)
Depthwise卷积是对input map的每一个通道进行单独的卷积,可以视为G=N的分组卷积操作的特例。
使用N个尺寸为K\times K\times 1的卷积核对尺寸为H\times W\times N 的输入feature map进行卷积,输出相同尺寸的feature map
计算成本为HWNK^2,通过忽略通道方面的卷积,depthwise卷积大幅减少了计算成本
Channel Shuffle

G=2时的Channel Shuffle操作 (Source: Yusuke Uchida’s blog post)

G=3时的Channel Shuffle操作 (Source: Yusuke Uchida’s blog post)
Channel shuffle是将input feature map的通道顺序进行随机打乱的一种操作。其操作主要通过reshape与transpose实现:
- 输入feature map尺寸为H\times W\times N,其中N=GN’
- 将输入reshape为H\times W \times G\times N’
- 将输入transpose为H\times W\times N’\times G
- 将输入reshape回H\times W\times N,作为输出
其计算成本无法用加法与乘法的操作次数来衡量,不过也是有一定开销的。
Efficient Models
ResNet & ResNeXt
对ResNet/ResNeXt的详细介绍可见之前的文章,这里主要介绍其卷积操作的结构。
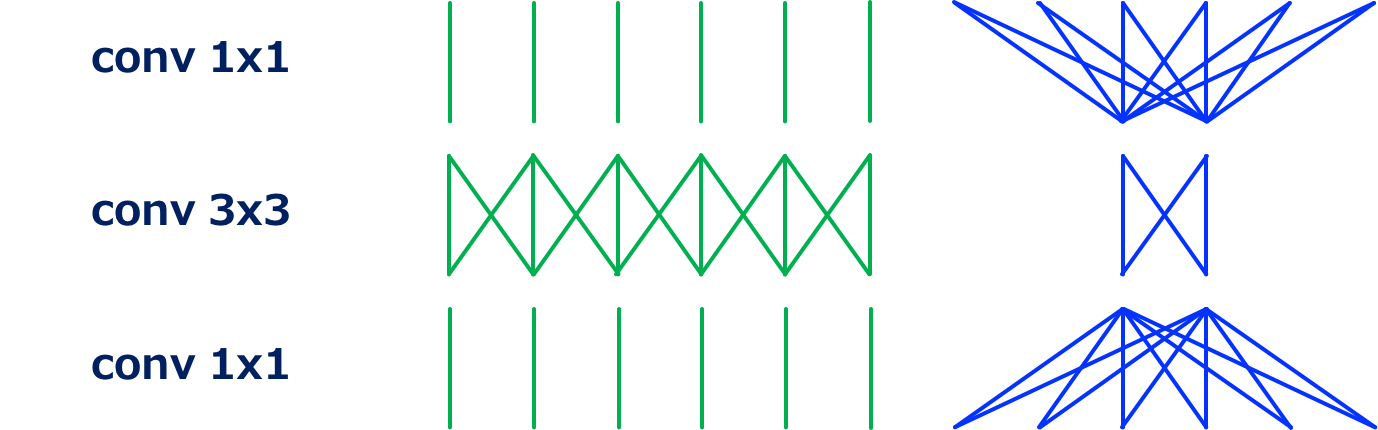
ResNet的bottleneck结构 (Source: Yusuke Uchida’s blog post)
ResNet的residual unit主要是一种bottleneck的结构,其能从一定程度上降低计算成本:
- 先用一个1\times 1的卷积减少输入的通道数,从而减少之后3\times 3卷积的计算成本
- 而后用3\times 3的卷积进行卷积
- 最后用1\times 1的卷积来恢复通道数

ResNeXt的bottleneck结构 (Source: Yusuke Uchida’s blog post)
ResNeXt的主要改进在于使用分组的3\times 3卷积代替了ResNet中的普通3\times 3卷积。如此一来,节省下的计算成本可以让第一步1\times 1卷积的通道缩减比率变得小一些,从而使得ResNeXt能在与ResNet相近的计算成本时获得更好的准确率。
SqueezeNet
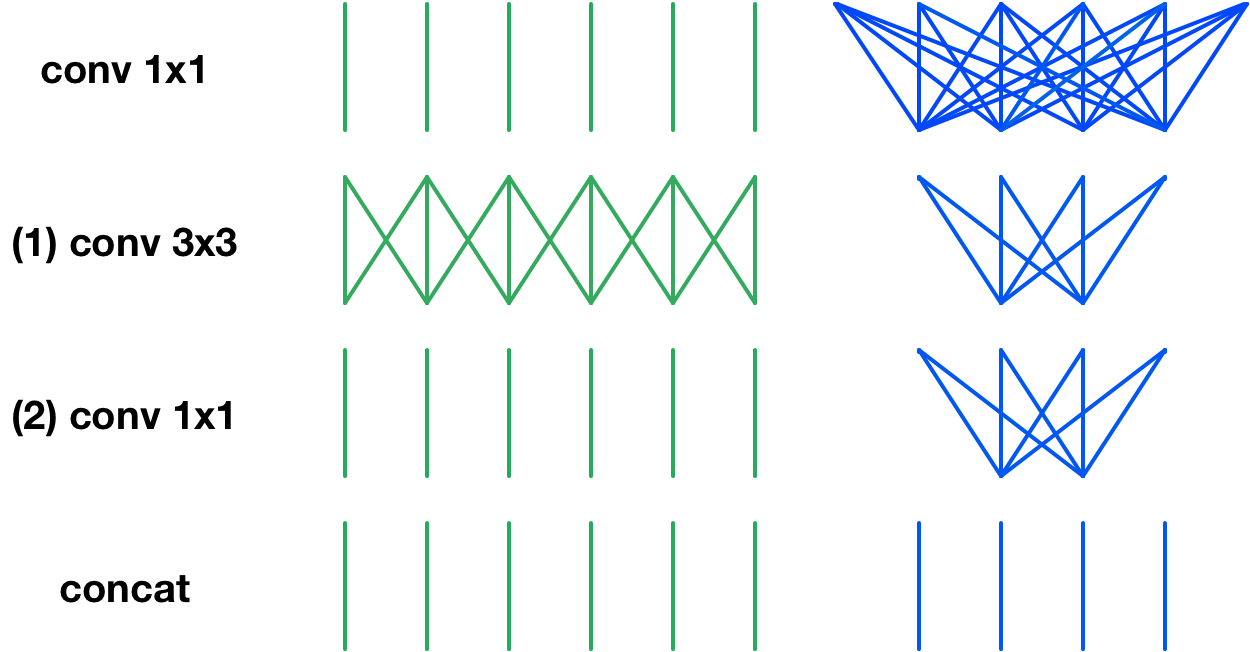
SqueezeNet的卷积结构
主要是改进了Inception的结构,提出所谓的squeeze + expand的fire module:
- 先用一个1\times 1的卷积减少输入的通道数,从而减少之后的计算成本
- 而后分别用1\times1与3\times 3的卷积进行卷积
- 在通道上连接上一步的两个输出结果
MobileNet
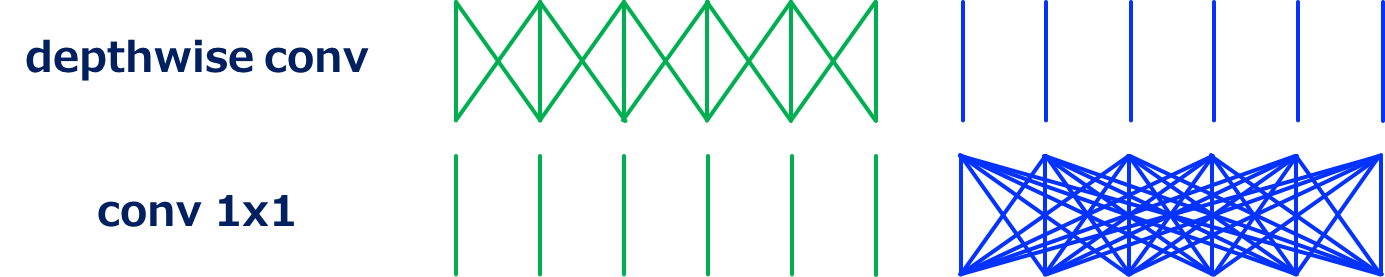
MobileNet的卷积结构 (Source: Yusuke Uchida’s blog post)
MobileNet主要是使用了separable convolution modules,也就是1个depthwise卷积加上1个pointwise卷积(也就是1\times 1卷积),使得卷积在空间与通道上的操作分离开来,从而显著地减少了计算成本。
- 首先使用depthwise卷积处理H\times W\times N的输入,其中使用了N个K\times K\times 1的卷积核,计算成本为HWNK^2
- 其次使用pixelwise的卷积处理上一步的输出,其中使用了M个1\times 1\times N的卷积核,计算成本为HWNM
所以1次separable卷积的计算成本为HWN(K^2+M),而普通的卷积操作的计算成本为HWNK^2M。由于一般情况下(例如M=32, K=3时),M\gg K^2,所以separable卷积的计算成本为普通方式的\frac{K^2+M}{K^2M}\approx\frac{1}{K^2},即大约$1⁄8或者1⁄9$倍。
同时,可以看出,此时的计算成本的瓶颈主要在于1\times 1卷积计算成本中的M因素。
ShuffleNet
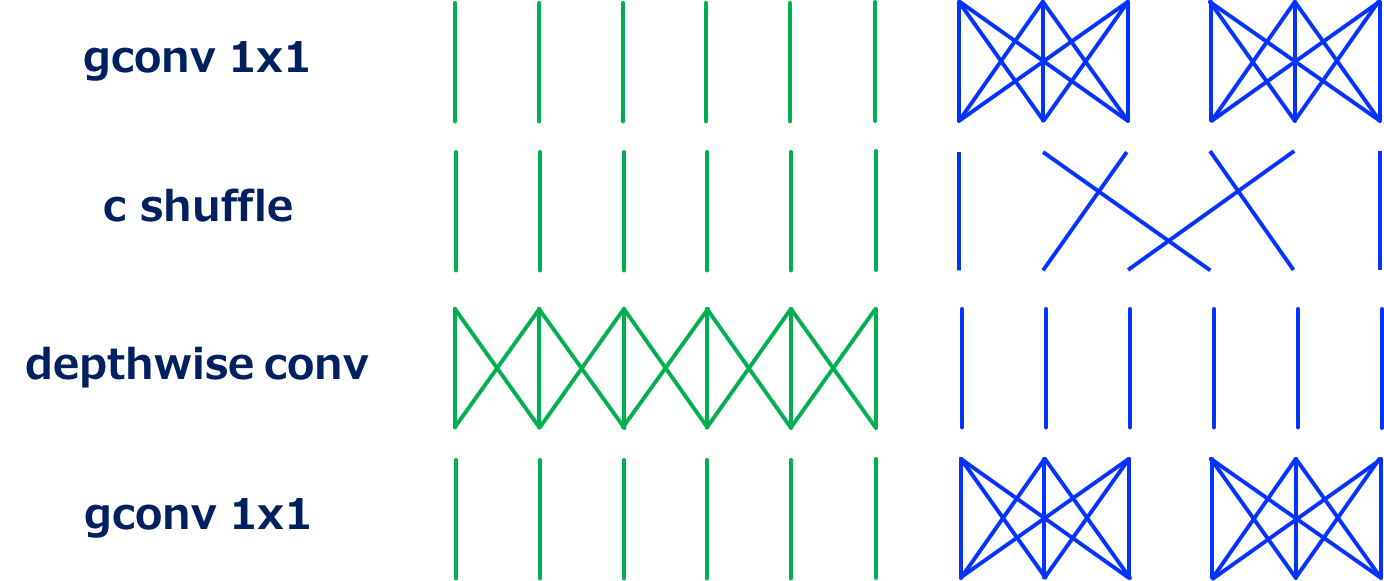
ShuffleNet的卷积结构 (Source: Yusuke Uchida’s blog post)
ShuffleNet主要是使用分组卷积来降低separable卷积操作中的1\times 1卷积的计算成本。同时,ShuffleNet还在分组卷积之后增加了channel shuffle操作,防止某一通道只在某一组中进行卷积,使得各个通道的输出都有可能传入到各个组中去,从而避免了精度降低。
MobileNet V2
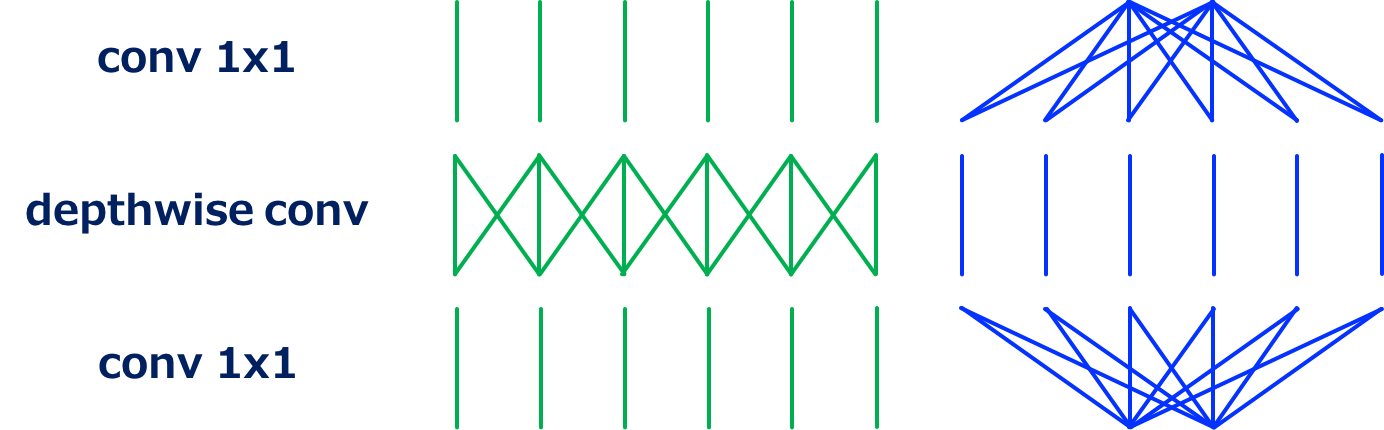
MobileNet V2的卷积结构 (Source: Yusuke Uchida’s blog post)
MobileNet V2主要在ResNet的residual unit的基础上,
- 使用depthwise卷积替换了普通的3\times 3卷积
- 使用1\times 1卷积首先扩大通道数,而后在最后减少通道数
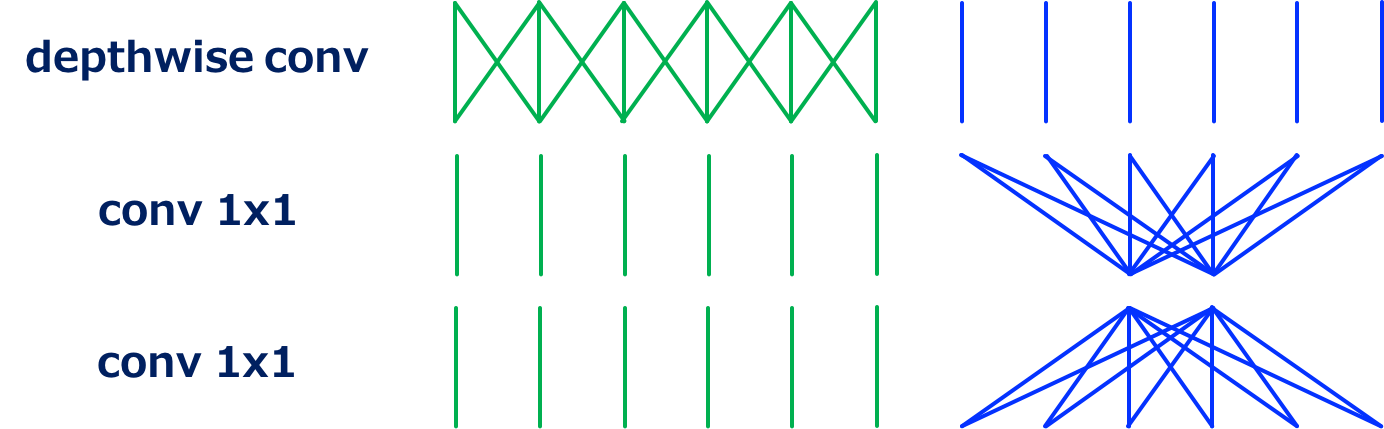
MobileNet V2的卷积结构的另一种表示 (Source: Yusuke Uchida’s blog post)
当然,MobielNet V2的unit也可以表示成如上图这样的形式(由于MobileNet V2是由一堆units叠在一起的,所以可以这么看)。这样的话,原始版本的MobileNet中的1\times 1卷积就被拆成了两个。令T表示通道数的减小比率,则原始的1\times 1卷积的计算成本为HWN^2,拆成2个1\times 1卷积的计算成本为2HWN^2/T。MobileNet V2使用T=6,则其1\times 1卷积的计算成本是MobileNet V1的$1⁄3$。
SqueezeNeXt
ShuffleNet V2
ShuffleNet V2主要是通过实验研究了在设计与评价轻量级网络的方法,并从中归纳了一些经验性的准则。
首先是直接指标(例如速度)与间接指标(例如 FLOPs)之间的差异。由于FLOPs仅和卷积部分相关,尽管这一部分需要消耗大部分的时间,但其它过程例如数据I/O、数据重排和元素级运算(张量加法、ReLU等)也需要消耗一定程度的时间。FLOPs近似的网络也会有不同的速度。这两者的差异主要在于:
- 对速度有较大影响的几个重要因素对 FLOPs 不产生太大作用。
- 其中一个因素是内存访问成本 (MAC)。在某些操作(如组卷积)中,MAC 占运行时间的很大一部分。对于像 GPU 这样具备强大计算能力的设备而言,这就是瓶颈。在网络架构设计过程中,内存访问成本不能被简单忽视。
- 另一个因素是并行度。当 FLOPs 相同时,高并行度的模型可能比低并行度的模型快得多。
- FLOPs 相同的运算可能有着不同的运行时间,这取决于硬件平台以及其网络实现。
通过实验研究,该文章提出了评价与设计的经验准则:
- 评价准则:
- 应该用直接指标(例如速度)替换间接指标(例如 FLOPs)
- 这些指标应该在目标平台上进行评估。
- 设计准则:
- 相同的通道宽度可最小化MAC
- 过度的组卷积会增加 MAC
- 网络碎片化(例如GoogLeNet或者Inception的多路径分支结构)会降低并行度
- 元素级运算的计算成本不可忽视
基于此,该文章提出了ShuffleNet V2的单元结构:
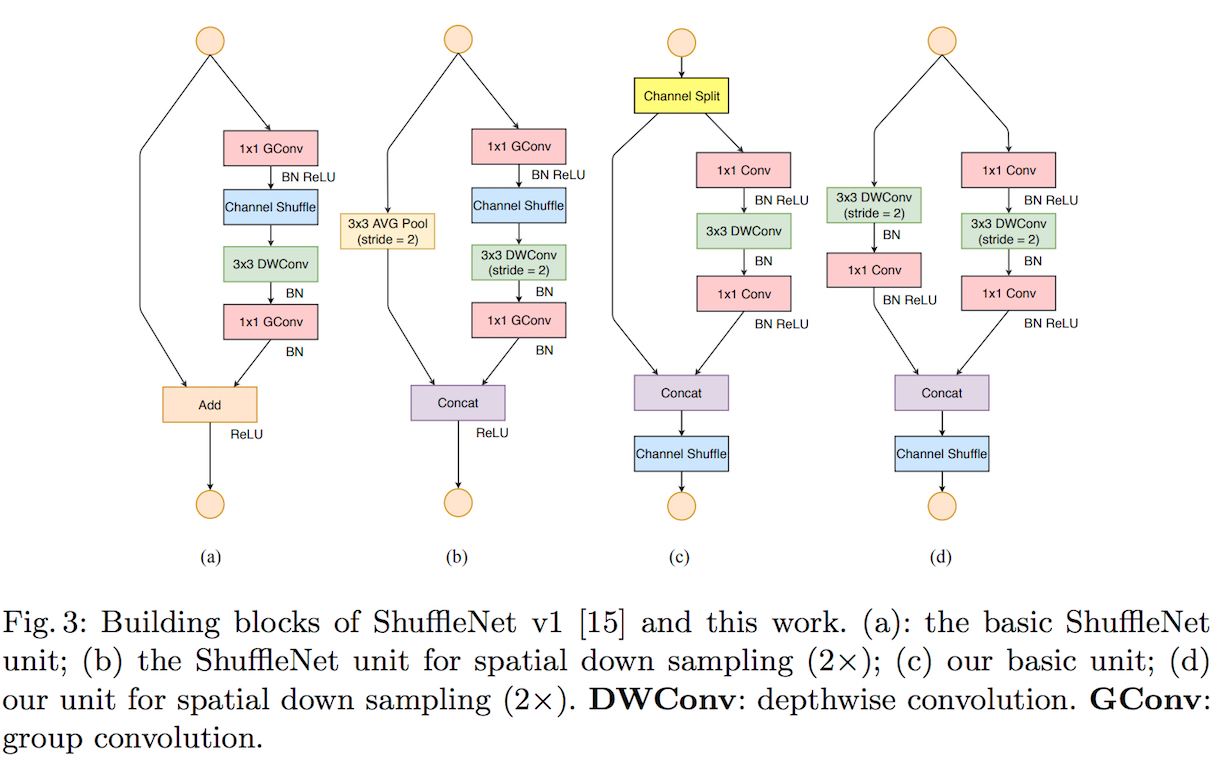
ShuffleNet V2的卷积结构 (Source: original paper)
Cheat Sheet