Notes for Amortized Inference and Learning in Latent CRF
Contents
This is my notes for Amortized Inference and Learning in Latent Conditional Random Fields for Weakly-Supervised Semantic Image Segmentation.
Introduction
CRF属于判别式的图模型,通常被用来标注或分析序列资料。2014年左右的时候,CRF也被用来做图像分割。但是随着深度学习的兴起,CRF慢慢就沦为了进行post-precessing的工具,以优化结果。一般的做法就是用分割网络输出的pixel-level的各类的概率分布作为CRF的unary potential,然后用*Efficient inference in fully connected CRFs with Gaussian edge potentials*里面的方法来设置pairwise potential。
强监督的语义分割用这个方法当然很好,但是弱监督的话,因为没有pixel-level的标签,要把image-level的标签有选择地广播到所有像素还是一个很艰苦的工作。通常用的方法是基于localization cues的,比如说用saliency maps、objectness priors或者bounding boxes等等,就像之前介绍的SEC一样。
不过这篇文章里面用的不是localization cues的那一套,而是把pixel-level的标签作为CRF的latent variables(隐变量),然后把图像本身以及image-level的标签作为observed variables(观测变量)。然后想通过训练inference network以估计在给定observed variables的情况下latent variables的后验分布(posterior distribution)这样的方法,把latent variables的inference cost分摊到整个数据集中。值得注意的是,这种方法并没有学习CRF的uanry potential,而是要训练inference network,使其输出的pixel-level标签在全局上与image-level标签一致,在局部上与附近的标签一致。
讲真上边这一句话我也读着不是很懂,慢慢看之后的说明就能理解了。
这种方法的好处在于,inference network(也就是分割网络)的训练可以是end-to-end的,并不需要另外去生成localization cues。此外,用这种方法训练出来的模型也不需要post-processing步骤。
这种方法的预测精度与使用了saliency masks的方法(比如说SEC)相近,也算是一种新的研究方向。
The proposed model
| Symbol | Description | Note |
|---|---|---|
| $x^{(i)}$ | 第$i$幅图像 | $1\le i \le n$ |
| $y^{(i)}$ | 第$i$幅图像对应的image-level标签 | Each $y^{(i)}$ is a boolean vector whose length equals the number of classes used for training. |
| $z^{(i)}=(z^{(i)}_j)$ | 第$i$幅图像对应pixel-level标签 | $1\le j\le m$, and we use one-hot encoding for $z^{(i)}_j$ |
本文的目标是,给定$(x^{(i)}, y^{(i)}), 1\le i \le n$的情况下,本算法希望能够学习到一个从$x^{(i)}$到$y^{(i)}$的映射关系,其能够对pixel-level的标注$z^{(i)}$做出推断。
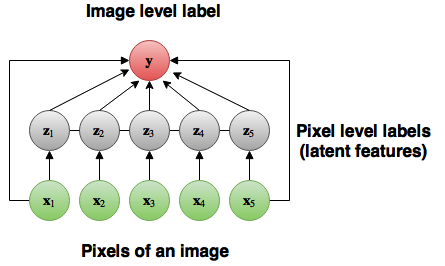
当给定图像$x$的时候,image-level的标签$y$的条件分布如下所示,目标则是能最大化$\sum^n_{i=1} log p(y^{(i)}|x^{(i)})$。 $$ p(y|x) = \sum_z p(z|x)p(y|z,x) $$ 定义$p(z|x)$为CRF的pairwise项,同时也是先验概率(Prior): $$ p(z|x) \propto exp \left(-\sum_{j<j’} k(t_j, t_{j’})\mu (z_j, z_{j’}))\right) $$ 其中$t_j$为位置$j$处像素的feature vector,$\mu (z_j, z_{j’})$为两个标签之间的compatibility。$p(z|x)$的意义在于使得相邻且色彩相似的像素具有同一标签。需要注意的是$p(z|x)$并不用训练,相反,需要学习的是作为CRF的unary potential的$p(y|z,x)$。
不过由于从$p(z|x,y)$进行采样在计算上十分困难,因此不能用EM法来最大化$\log p(y|z,x)$,具体分析可见原论文。因此需要用其他方法来达成目的。该文章使用的方法是最大化$p(y|x)$的下界,来使得$p(y|x)$最大。
Variational Lower Bound
用了一个变分分布$q(z|x,y)$,通过以下变换得到了$\log p(y|x)$的一个下界:
$$
\begin{align}
\log p(y|x) & = \log \sum _z p(z|x) p(y|z,x) \
& = \log \sum _z q(z|y,x) \frac{p(y|z,x)p(z|x)}{q(z|y,x)} \
& \ge \sum _z q(z|y,x) \log \frac{p(y|z,x)p(z|x)}{q(z|y,x)} \
& = -KL(q(z|y,x)||p(z|x)) + E_{q(z|x,y)} \log p(y|z,x)
\end{align}
$$
下界的第一项使得变分分布$q(z|y,x)$趋向于与图像$x$的先验分布$p(z|x)$接近,也就是说,使得$q所产生的分割遮罩在一定程度上遵循图像中的位置信息与色彩信息。也就是保持了局部的一致性。下界的第二项则能够使得变分分布所产生的遮罩能够提升图像分类的得分,即确保了pixel-level的标签与image-level标签一致。
假设变分分布$q(z|y,x)$可以被完全地因式分解,其具体定义如下:
$$
q(z|x,y)= \prod _{j=1}^m q(z_j | y,x)
$$
$$ q(z_{jk}=1|x,y) = \frac{\exp (g_{jk}(x))}{\sum ^K_{k’=1} \exp (g_{jk’}(x))} \equiv \varphi_{jk} (x) $$
其中$g$是全卷积网络或者说是分割网络,${g_{jk}(x), 1 \le j \le m, 1\le k \le K }$则是$g$对$x$的输出。
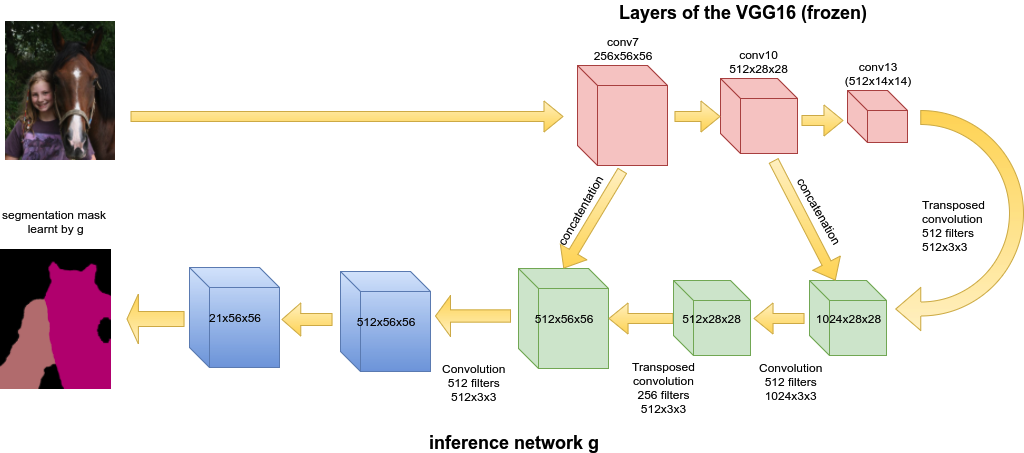
Gradient of the Lower Bound
下界的第一项其实是基于$g$的输出的KL散度损失,该损失的梯度可以精确计算出来的。第二项的梯度可以使用MCMC采样来估计。
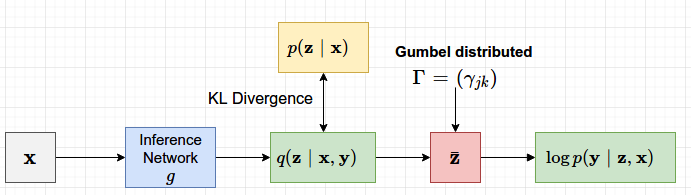
具体的推导过程可以看原论文的2.2节。
Experiments
在PASCAL VOC 2012上的表现很不错,能够与SEC等方法相媲美了。

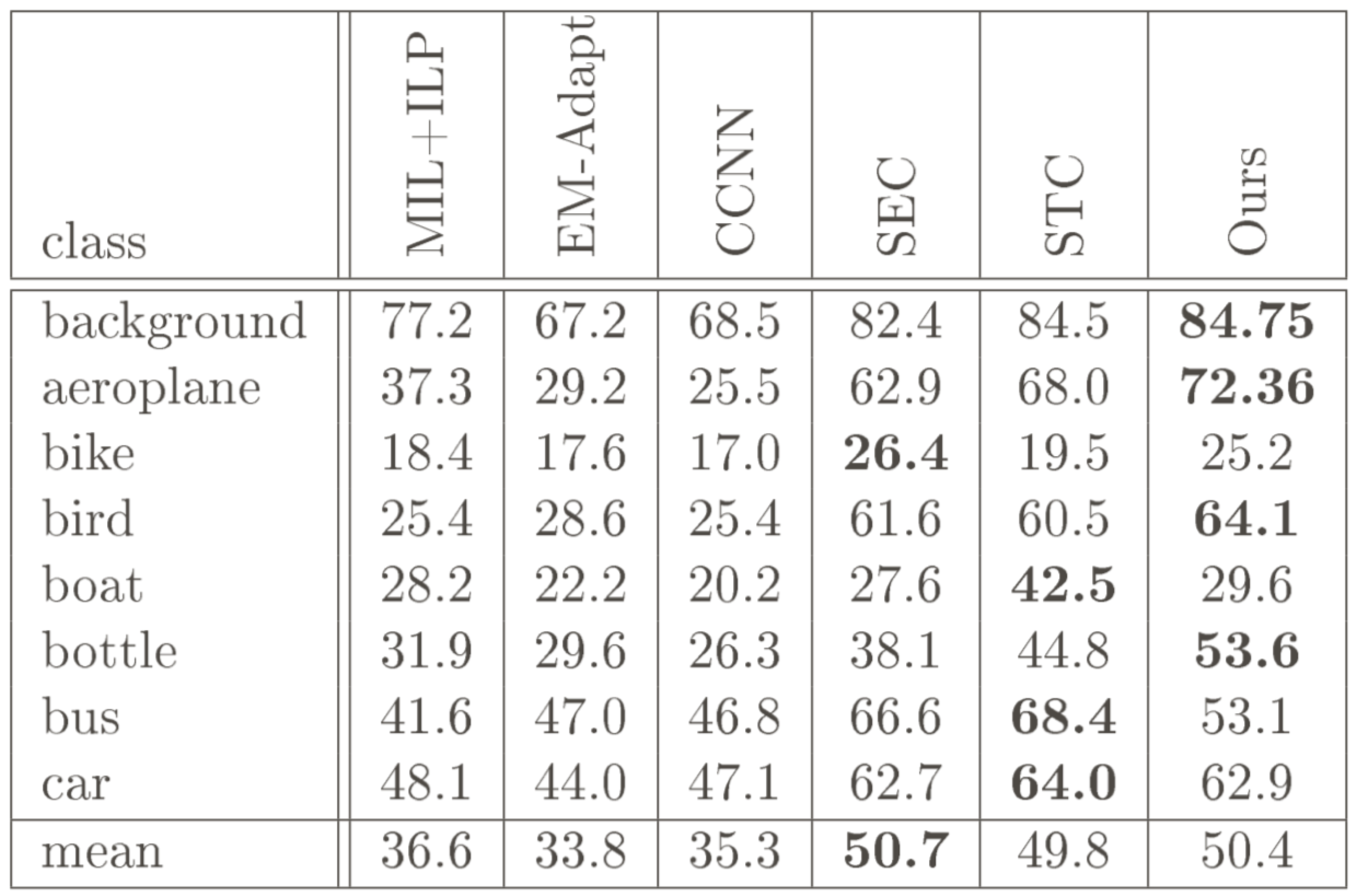
Conclusion
- 这是语义分割领域里面,第一篇在CRF中使用CNN来做inference network的文章,效果还很不错;
- 该方法相比所有的不用saliency maps的方法来说,结果都要好;
- 该方法的预测精度和用了saliency maps的方法相差无几
- 该方法表明传统的概率模型与CNN结合之后能得到很好的效果。
Future
个人感觉这篇文章所用的方法还是很有借鉴意义的,不用很多tricks,不靠saliency maps就能达到这么高的mIoU。可以改进的地方我想应该有两个,一个是$p(z|x,y)$的形式可以修改,比如说参考ScribbleSup的,把纹理、色彩、空间之类的低阶信息都考虑上。另外,$p(y_k |x,z)$的计算方式也可以修改。总而言之,这还是一片比较粗糙的文章,还有很多需要精雕细琢的地方。